Cerca
Statistiche
- Login per inviare commenti
In nessuno degli studi statistici che sono riuscito a reperire su internet ho trovato informazioni sulla distribuzione delle lesioni corporee a seguito di incidente stradale ne tantomeno ho trovato la correlazioni fra queste ed il tipo di equipaggiamento del motociclista coinvolto e l'esito dell'incidente stesso.
Per il momento l'unica informazione del genere che in via indiretta sono riuscito a recuperare riguarda le lesioni neurologiche permanenti sulla spina dorsale che dovrebbero ammontare al 2% del totale delle lesioni alla colonna. Però non ho trovato specificato la percentuale di lesioni sulla colonna a seguito di incidente (e magari che tipo di incidente!) ne tantomeno se l'infortunato portasse o meno il paraschiena e di che tipo.
Penso che avere dati del genere sia estremamente interessante anche per valutare concretamente i rischi connessi all'uso della moto ed il tipo di protezioni ragionevolmente raccomandabili.
Sapete se esistono pubblicazioni di questo tipo, anche a pagamento?
Ciao.
I dati sicuramente esistono perche' c'e' una branca dell'ingegneria che si occupa di incidenti stradali, simulando e ricostruendo l'accaduto. Se devo pero' essere sincero non mi e' mai capitato di trovare dati in proposito.
Anche perche' presumo che le lobby nel caso specifico siano talmente potenti da occultare i risultati; e se venisse fuori che il veicolo A ha una incidenza di gravi infortuni maggiore del veicolo B, o lacune specifiche a carico dell'equipaggiamento C...?!?!?
Lo so, sono diffidente per natura.... 
cercando qualcosa si trova
il mio piccolissimo contributo è questo poi vi spiego perchè l'ho messo
http://www.fondazioneania.it/fondazione/fondazione/export/sites/default/...
i prodotti difettosi per il grande pubblico (le auto, per intenderci) vengono "beccate" sempre più (basti notare le campagne di richiamo sempre più numerose olte al contributo dei crash test)
ho messo quel link perchè, ad oggi, la prima causa degli incidenti è dovuta a comportamenti sbagliati.
dal momento che soprattutto in moto le "barriere" protettive che utilizziamo portano un contributo minimo (non lo dico in chiave critica anzi, è solo "fredda" logica) e penso al paraschiena e al casco che DEVONO ESSERE SEMPRE USATI ma non possono fare miracoli - mentre le cazzateche si fanno producono la maggior parte del danno, è opportuno partire da ciò che produrrebbe i migliori risultati.
Gli italiani alla guida fanno mediamente molto schifo, guidano dimenticando che GUIDARE E' LA'TTIVITA' PIU' PERICOLOSA (NEL SENSO DI LETALE) e vanno in auto e in moto con livelli di "leggerezza" che non hanno nemmeno quando usano il coltello per sventrare un pesce.
Non volevo fare dietrologia penso solo - per quanto l'idea di raccogliere dati sia non buona ma ottima - che allo stato attuale si debba partire da info generiche (tipo: "se pensi ai cazzi tuoi, spippoli il cellulare o altre ca***te quando guidi, bello mio rischi di morire") e solo in un secondo momento, e per gente già "preparata", proporre info e statisitche di dettaglio per spingere l'uso dei sistemi di protezione indivuduale.
Questo perchè si rischia di far passare il messaggio "mettiti un bel casco e il paraschiena e poi fai come ti pare".
Potrei essermi espresso in modo poco chiaro - sapete, la foga... - ma ribadisco che l'idea di cercare le statistiche è ottima, solo c'è da chiedersi cosa realmente possa essere utile hic et nunc e poi procedere per gradi.
roadsafety.mccofnsw.org.au 
è pieno
anche qua e nelle pagine collegate
http://ec.europa.eu/transport/road_safety/specialist/knowledge/poweredtw...
ma anche l'ISTAT dovrebbe avere qualcosa
senza link o altro....ho fatto lo screen di un lavoro. 
da notare che, usando abb. cert. ce, con ogni probabilità la percentuale di essere injured scende ancor meno rispetto alla tabella. Facendo un ragionamento teorico (vedi anno) 
Avevo scaricato e mi sono iscritto come motosicurezza a un coso che si occupa di queste cose... non mi ricordo più come si chiama però... Ogni mese mi mandano anche una newsletter... Poi non ho letto i report, ma appena sono sull'altro computer metto il link...
una volta avevo letto questo: http://www.acem.eu/PPE/html/IT_eSUM_ppe.pdf
è secondo me molto approssimativo e rozzo nell'analisi e nella classificazione degli indumenti "protettivi"
vi rigiro il commento di P. Varnverry. Praticamente dice che il documento andrebbe eliminato dalla circolazione a causa dei gravi errori ed omissioni. Segato è una persona che lavora all'ACEM o giù di lì. Tra l'altro non si dice che protettivo=certificato
Thank you for advising me of the publication of this new document.
It is a very disappointing publication due to a very significant flaw, which leaves it open to accusations of being misleading to the motorcycling consumer.
Apart from reference to standards for motorcyclists’ safety helmets and a very brief mention on page 12 that “Protectors must be CE marked as a proof of compliance with EU standards”, the publication fails to make any mention whatsoever of the existence of European norms EN 13594, EN 13595 and EN 13634.
Either the authors of the document have failed to adequately research the matter or they have deliberately withheld reference to these standards. Either way, the sponsors of the document should have checked the content before approving its publication. They have consequently failed to accomplish the objective of providing “some simple guidelines supported by scientific evidence to help increasing the number of motorcyclists equipped with appropriate protective clothing.”
The document should be withdrawn from circulation with immediate effect and not reissued until the serious errors and omissions described above have been corrected.
Regards,
Paul Varnsverry
(Member of CEN TC 162 WG11 and leader of the project group responsible for finalisation of EN 13595)
senza link o altro....ho fatto lo screen di un lavoro. 

da notare che, usando abb. cert. ce, con ogni probabilità la percentuale di essere injured scende ancor meno rispetto alla tabella. Facendo un ragionamento teorico (vedi anno) ;)
utilissimi i grafici e le statistiche, fate solo attenzione a cosa comunicano "veramente" e a come comunicano, o si corre il rischio di letture "al contrario".
per esempio, io che faccio fatica con la statistica - e sono in buona compagnia per quanto ne so - e guardo la colonna del lower body, vedo che indossare abbigliamento protettivo diminuisce del 6% la probabilità di essere injured.
allora potrei chiedermi: vale la pena di spendere centinaia di euro per abbigliamento in pelle o "protettivo" - crepando dal caldo - al posto di un più comodo paio di jeans, per ridurre del 6% la probabilità di essere "injured"?
è chiaro ciò che voglio dire? attenzione a fidarsi troppo delle statistiche e affidare a loro messaggi importanti: la gente le può interpretare alla ca*** pur con tutta la buona volontà.
sto solo facendo l'avvocato del diavolo, ora non accanitevi contro di me  io sono già convinto
io sono già convinto 
cito un pezzo di una mia riflessione (http://www.motosicurezza.com/?q=blog/riflessione-personale-movimento-ant...) dove parlo di statistiche
"He [Munich, Schuller et al. 1986] concluded that motorcycle clothing is
significantly effective in preventing or reducing at least 43% of injuries to the skin
and soft tissue with a 63% reduction in deep and extensive injuries.
More recently Otte et al (2002), has found that riders wearing protective clothing
had significantly fewer leg injuries in crashes at the same relative speed (eg 40%
vs 29% injury free at speeds between 31-50 km/ph). He also identified a
significant benefit in reduction of foot injuries for riders wearing high boots.
Overall he also reported that riders without protective clothing sustained injuries
in collisions at lower speeds (80% at < 50 km/h compared to 80% <60 km/h for
riders with protective clothing)."
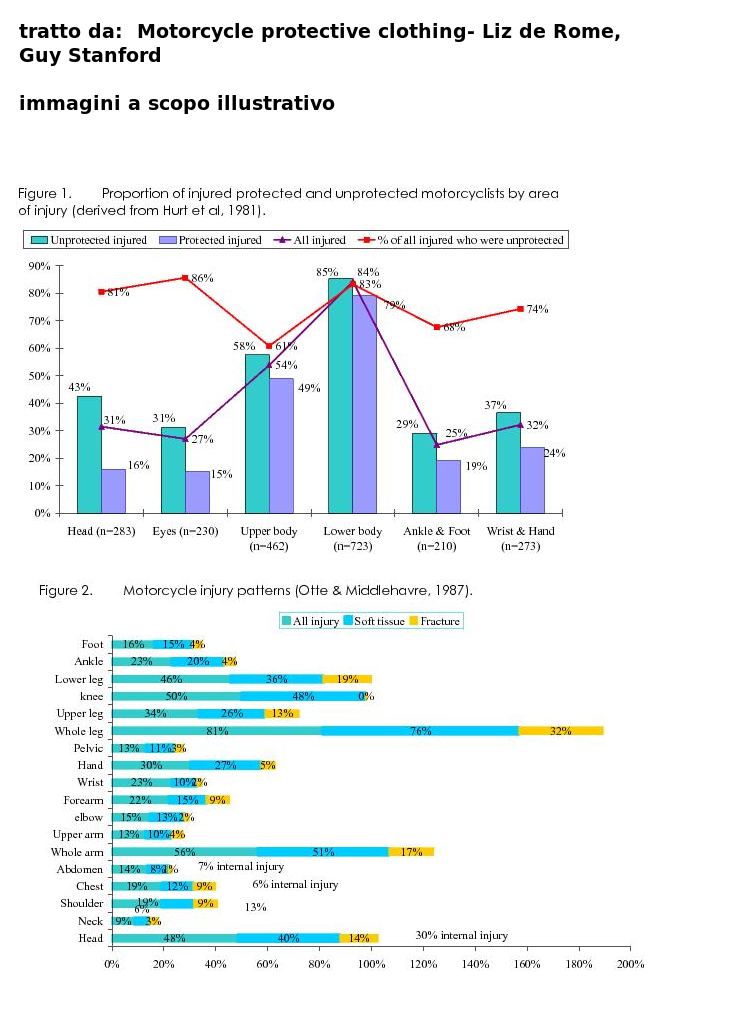
Quindi si parla di una FORTE riduzione statistica, benchè nello stesso documento da cui ho citato (Motorcycle protective clothing - Autori: Liz de Rome, Presenter, Guy Stanford - Anno: 2003), si dica di come non si prevengano il rischio di penetrazione e altri rischi (si tratta tuttavia di uno studio più "antiquato" (EEVC, 1993).
Sì era l'Acem.eu...

Invece io, che di statistica ne ho masticata un po', non ho la piu' pallida idea di come leggere il primo grafico. Che significa?!
Le barre sono percentuali >>di cosa<<?
Come fa la linea viola, che rappresenta, ipotizzo, la popolazione di feriti, essere espressa in percentuale? Di nuovo: percentuale di cosa?
E come fa il sottoinsieme di feriti non protetti ad essere sempre superiore alla linea della popolazione (tutti i feriti)?
Tra l'altro, il titolo parla di "proporzione". Tra che e che? Se fosse tra feriti e non feriti, la somma dovrebbe essere 100% su ogni barra, o sul "totale". Ma nessun conto torna...
Non capisco letteralmente nulla. Ho come l'impressione che abbiano sovrapposto grafici basati su sistemi di riferimento diversi (improbabile) o di non aver capito nulla. Qualcuno ha capito?
Edit:
La linea viola "All Injured" è tracciata come media dei valori di ciascuna coppia di barre. Non so in che modo possa rappresentare "tutti i feriti".
La linea rossa rappresenta, dice la legenda, la percentuale dei feriti che erano non protetti, e questo parrebbe un conetto chiaro: su 100 feriti alla testa (prima coppia di barre e primo punto della linea rossa) 81 erano senza protezione (mi sembra un dato alto, ma 30 anni fa, periodo a cui si riferisce il grafico, immagino che fosse plausibile). La cosa è in contraddizione completa con la barra celeste (43% e non 81%). Inoltre la barra corrispettiva viola (feriti protetti) 16% non porta la percentuale a 100 n[ se sommata a 43, n[ se sommata ad 81. E lo stesso accade per il resto del grafico.
Boh. 
oddio sarò ingenuo io ma lo ho capito.
esempio preso dal teso:
"For example, 31% of all motorcyclists suffered head injuries, but
these included 43% of those who were not wearing helmets compared to
only 16% of those who were. In all, 81% of all those who sustained head
injuries, were unprotected."
Si, spero che il testo contenga qualche spiegazione. Dov'e', per curiosita'? Mi e' sfuggito forse il link?
Il grafico, preso da se, continua a sembrarmi confuso e scorretto.
Il tuo esempio tratto dal testo sembra darmi ragione: hanno preso percentuali che si riferiscono a popolazioni diverse e le hanno incredibilmente sbattute sullo stesso grafico, con un'asse delle ordinate unico.
Traduco:
"Per esempio il 31% di tutti i motociclisti (la popolazione A, in senso statistico, considerata. Immagino che nel testo si spieghi se si tratti di tutti i motociclisti al mondo, in UK, in EU, o che so io. Sarebbe cmq interessante capirlo, ma cmq diciamo "tutti") ha subito ferite alla testa."
Ok, chiaro. Mi sembra un valore altino, ma bene cosi'. Proseguo:
"... ma questi (il 31% ferito) includevano sia il 43% di coloro che non indossavano il casco rispetto al solo 16% di oloro che lo indossavano"
Ok. Chiaro. Qundi abbiamo 3 popolazioni e tre percentuali che si riferiscono a ciascuna popolazione rispettivamente. Quindi come fanno a stare sullo stesso grafico senza creare un caos completo?
- Su 100 motociclisti, 31 ha subito ferite alla testa.
- Su "100 motociclisti che non indossano il casco" (una diversa popolazione B) 43 sono finiti nella percentuale di feriti precedente (31), mentre solo 16 di coloro che lo indossavano (altra popolazione ancora C) ci sono finiti.
Su questa base, il grafico e' gia' sbagliato perche' la percentuale della poplazione A (tutti i motociclisti) non e' paragonabile/sovrapponibile a quella della popolazione B (i motociclisti che indossano il casco) e della poplazione C (coloro che non lo indossano). Manca la relazione tra le tre popolazioni. Stabilita questa relazione allora le percentuali andrebbero ricalcolate e solo poi messe su uno stesso grafico. In altre parole se sulle ordinate hai la percentuale della popolazione A, essa non puo' essere numericamente la stessa per la popolazione B e C ed il grafico perde ogni senso.
"Nel complesso, l'81% di coloro che hano subito un incidente alla testa erano sprotetti"
Ok. Una quarta popolazione a cui si riferisce ora quell'81 %: popolazione D (quelli che hanno subito un danno alla testa)
Insomma, come sospettavo, hanno preso percentuali di ben 4 popolazioni diverse e le hanno sbattute in un unico grafico.
Ma chi sono questi? Imbarazzante.
Cmq, Alax, grazie del testo. Ora capisco cosa intendono. E quel grafico e' da buttare 
Tanto per chiarir(mi/ci) questo guazzabuglio ( ) di numeri, ricalcolo le percentuali rendendole comparabili:
) di numeri, ricalcolo le percentuali rendendole comparabili:
Su 100 motociclisti:
- 31 hanno subito ferite alla testa, di cui 25 (81% di 31) non aveva il casco e 6 (restante 9% di 31) lo aveva.
- 58 non indossano il casco (dei quali 25, il 43% di 58, si e' ferito alla testa) e 37 lo indossano (dei quali 6, il 16% di 58, si e' ferito).
- Ne mancano 5 che non ricadono ne' tra coloro che hanno il casco ne' tra coloro che non lo hanno; le cose non tornano anocra copletamente, e "non so che abbiano in testa": saranno gli autori...  Sara' un qualche errore o chi puo' dirlo.
Sara' un qualche errore o chi puo' dirlo.
Miseriaccia che casino. Sembra un giochino matematico della settimana enigmistica, invece che dati illustrativi. Il grafico, poi, a parte suggerire l'idea che "chi si protegge si ferisce meno" e' completamente errato.
Per curiosita': autori, fonte, chi ha commissionato lo studio?
Per il momento vi ringrazio per i links, spero di trovare esattamente ciò che cerco. Sono di corsa e non ho tempo per soffermami sugli spunti del thread, sicurament elof arò in settimana. Contribuisco però a citare uno studio che ho trovato molto interessante anche se ciò che mi interessa è trattato marginalmente:
Ciao.
@ taym: lo studio è di hurt (quando si dice il nome...  ) e fidati che è uno degli studi migliori. il nome è: Hurt, H. H. Jr., Ouellet, J.V. & Thom, D.R. (1981), "Motorcycle Accident Cause Factors and Identification of Countermeasures", Final Report to the National Highway Traffic Safety Administration, US Department of Transportation, PB 81-206443, 81-206450.
) e fidati che è uno degli studi migliori. il nome è: Hurt, H. H. Jr., Ouellet, J.V. & Thom, D.R. (1981), "Motorcycle Accident Cause Factors and Identification of Countermeasures", Final Report to the National Highway Traffic Safety Administration, US Department of Transportation, PB 81-206443, 81-206450.
Il problema è che il grafico è stato fatto su base di questo studio da...canguri (  ) ovvero: http://www.roadsafety.mccofnsw.org.au/ (è uno delle "references", ma non ricordo quale -lo ho scaricato ma ora mangio :P- ) il terzo "de rome"
) ovvero: http://www.roadsafety.mccofnsw.org.au/ (è uno delle "references", ma non ricordo quale -lo ho scaricato ma ora mangio :P- ) il terzo "de rome"
Questo studio “dimostra” che è necessario proteggere testa, occhi, piede-caviglia e mano-polso, mentre il resto del corpo non trae beneficio significativo dalla protezione.
Quando le linee spezzate rossa e viola si toccano, vi è una sostanziale indifferenza tra l’essere protetti o non esserlo.
83% (di tutti i motociclisti feriti) aveva ferite al lower body (include il bacino?)
85% (di tutti i motociclisti feriti non protetti) aveva ferite al lower body
79% (di tutti i motociclisti feriti protetti) aveva ferite al lower body
…andiamo male….
Mi permetto di ribadire “attenzione a cosa le statistiche comunicano davvero a chi le legge”.
Qui è molto importante segnalare che lo studio, pur se ben condotto metodologicamente, paga lo scotto della sua vetustà. Abbigliamento certificato immagino ai tempi ce ne fosse zero, e forse anche paraschiena e simili erano pressoché ignoti.
Questo probabilmente spiega i dati delle due colonne centrali.
Con dati più recenti molto probabilmente si osserverebbe un maggior beneficio della protezione anche per upper e lower body.
Dimifox & all,
le info che cerchi credo di averle trovate in una specie di libro che, a mio parere, analizza a 360° il tema della sicurezza in moto con attenzione e chiarezza.
Forse qualcuno già lo conosce, io l'ho trovato per caso e spero possa essere di aiuto per chi come me ha ancora dei dubbi o ignoranza rispetto tutto ciò che vuol dire essere in sicurezza in moto.
Ecco il link: http://www.visionzero.org/blog/arte-della-sicurezza-in-moto
Ps: ovviamente motosicurezza è il mio sito di riferimento 
Ciau!!
No, attenzione, la linea viola rappresenta coloro che >non< indossavano la protezione, quindi quando si toccano semmai significherebbe il contrario, se non fosse che, ancora più attenzione, il grafico è sbagliato: la linea rossa e la linea viola non si toccano mai in realtà, perchè appartengono a sistemi di riferimento diversi e sono state erroneamente poste nello stesso sistema di assi. In altre parole il grafico è del tutto sbagliato.
In particolare, correggendo il grafico nel punto in cui le linee si toccano - in modo analogo a come fatto sopra - si avrebbe che:
Su 100 motociclisti
- 83 hanno subito danni alla parte bassa del corpo (linea rossa) di cui 70 non indossavano protezione - linea viola (84% di 83, approssimato). Quindi in quel punto le due linee non si toccherebbero mai, perchè una avrebbe un valore di 83 e l'altra di 70 (invece che addirittura 84 come nel grafico).
Già le statistiche vanno capite prima di formarsi un'opinione. Se poi fanno sta roba... Diamine.
In particolare, correggendo il grafico nel punto in cui le linee si toccano - in modo analogo a come fatto sopra - si avrebbe che:
Su 100 motociclisti
- 83 hanno subito danni alla parte bassa del corpo (linea rossa) di cui 70 non indossavano protezione - linea viola (84% di 83, approssimato). Quindi in quel punto le due linee non si toccherebbero mai, perchè una avrebbe un valore di 83 e l'altra di 70 (invece che addirittura 84 come nel grafico).
Già le statistiche vanno capite prima di formarsi un'opinione. Se poi fanno sta roba... Diamine.
Taym sei sicuro?... la posizione reciproca delle due spezzate sul grafico sarà correlata in qualche modo ai dati di origine...e cmq, se fosse come dici tu, per converso, vista la differenza tra le "posizioni delle due curve nella zona delle ferite a testa piedi e mani, parrebbe addirittura che usare i dispositivi di protezione, in questi casi, riduca il rischio in maniera non significativa...
oppure ancora, come dici tu, il grafico è del tutto sbagliato...
in entrambi i casi... direi che non centra molto l'obiettivo di favorire la cultura e l'uso delle protezioni... o no? 
Certo, ma il problema è che il grafico non tiene conto di questa correlazione. Se noti tutte le curve e le barre sono proporzionali al >loro valore percentuale numerico< come indicato sull'asse Y. Ma si tratta di percentuali >>di popolazioni diverse<< e dovrebbero essere ricalcolate prima di essere su uno stesso grafico.
Ad esempio, considera le linee che hai menzionato:
La "Percentuale di tutti gli utenti feriti" - ovvero, su 100 motociclisti quanti si sono feriti - linea viola, non può numericamente essere accostata alla "percentuale di utenti feriti sprotetti" - su 100 motociclisti feriti (che non sono i 100 motociclisti di prima: mica tutti si feriscono) quanti erano sprotetti - , linea rossa.
Ma, nel grafico, come noti, 84% di una linea è vicino all'83% dell'altra, per esempio, quando sono grandezze del tutto diverse. E' insensato accostarle prima di ricalcolarne i valori.
e cmq, se fosse come dici tu, per converso, vista la differenza tra le "posizioni delle due curve nella zona delle ferite a testa piedi e mani, parrebbe addirittura che usare i dispositivi di protezione, in questi casi, riduca il rischio in maniera non significativa...
Già, parrebbe, ma non è, perchè sono percentuali che siriferscono a popolazioni (i "100") diverse e il loro avvicinarsi o allontanarsi non dice nulla di chiaro.
Considera questo esempio assurdo:
il 25% degli utenti della strada (macchine, moto, biciclette, pedoni) ha avuto un incidente con ferite.
il 25% dei motociclisti compra una BMW 1200GS.
Metti tutto sullo stesso grafico e vedrai che ne risulterà, confrontanto le due linee, che tutti i possessori di 1200GS hanno avuto incidenti con ferite.  Che senso ha?
Che senso ha?
Ovviamente devi prima calcolare che percentuale di utenti della strada è motociclista. Sulla base di quel valore calcolare quanti sono i motociclisti con 1200 GS. Poi vedere quanti su 1200 GS sono feriti, calcolarne una percentuale su base comune con gli utenti della strada, e metti tutto sullo stesso grafico.
In altre parole se metti percentuali sullo stesso grafico, i "100" di riferimento devono essere gli stessi! 
in entrambi i casi... direi che non centra molto l'obiettivo di favorire la cultura e l'uso delle protezioni... o no? :~
Beh, l'unica indicazione sensata che vedo nel grafico è che, confrontanto le coppie di barre (e ignorando le linee), gli sprotetti si feriscono di più; ma non si capisce su che base. Come dicevo ad Alax, ovviamente il testo chiarirebbe le intenzioni del grafico, e mostrerebbe anche come sia stato disegnato con errori tali da rendere insignificanti le proporzioni tra i suoi stessi elementi.
Ad esempio, se guardi a sinistra ne grafico, vedi che su 100 utenti "31 si sono feriti" - quindi 69 NON si sono feriti, sono sani - ma, al contempo, 43 si sono feriti senza casco  . Come è possibile?
. Come è possibile?  Al massimo i feriti senza casco potrebbero essere tutti i feriti, ovvero 31. Per di più sappiamo che, seppur meno, si ferisce anche qualcuno col casco, quindi i feriti senza casco dovrebbero essere >necessariamente< minori o uguali a 31; non 43!
Al massimo i feriti senza casco potrebbero essere tutti i feriti, ovvero 31. Per di più sappiamo che, seppur meno, si ferisce anche qualcuno col casco, quindi i feriti senza casco dovrebbero essere >necessariamente< minori o uguali a 31; non 43!
adesso mi stampo la tua risposta e me la studio  e ci risentiamo tra un paio di settimane
e ci risentiamo tra un paio di settimane 
vorrei citare:
Martin Gardner, the American mathematics and science writer who became famous for his “Mathematical Games” column in Scientific American from 1956 to 1981, once said that “in no other branch of mathematics is it so easy to experts to blunder as in probability theory”.
figuriamoci i non esperti come me 
Dal testo esplicativo di Alax e dalla legenda, direi che il grafico corretto delle due curve dovrebbe essere cosi':
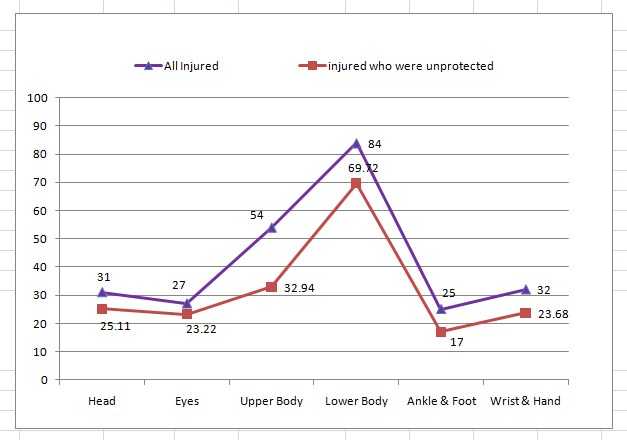
Nota che ora emerge come, dato un numero di feriti, la maggiorparte di essi fosse senza protezione.
Non ho modo di inserire le due barre, perche', dal testo di Alax, non si capisce, in totale, che percentuale di motociclisti usi le protezioni e che percentuale no. Siappiamo quale percentuale di coloro che non usano protezioni si feriscono, e che percentuale di coloro che le usano si feriscano, ma e' un dato diverso. Per legarlo ed inserirlo nel grafico c'e' appunto bisogno dell'informazione mancante che dicevo.

Nota che ora emerge come, dato un numero di feriti, la maggiorparte di essi fosse senza protezione.
Non ho modo di inserire le due barre, perche', dal testo di Alax, non si capisce, in totale, che percentuale di motociclisti usi le protezioni e che percentuale no. Siappiamo quale percentuale di coloro che non usano protezioni si feriscono, e che percentuale di coloro che le usano si feriscano, ma e' un dato diverso. Per legarlo ed inserirlo nel grafico c'e' appunto bisogno dell'informazione mancante che dicevo.
Quando ti ci metti sei sempre uno spettacolo..... 
Grazie dell'apprezzamento, ma davvero sono 5 minuti di orologio su Excel. Il merito è piuttosto poco.

Piuttosto, appena ho un minuto mi piacerebbe leggere lo studio così da ottenere il dato che manca ed inserire le barre. Potrebbe essere interessante, anche se si tratta di dati di 30 anni fa su tecnologie protettive che, immagino, siano spesso superate.
Grazie dell'apprezzamento, ma davvero sono 5 minuti di orologio su Excel. Il merito è piuttosto poco.

Piuttosto, appena ho un minuto mi piacerebbe leggere lo studio così da ottenere il dato che manca ed inserire le barre. Potrebbe essere interessante, anche se si tratta di dati di 30 anni fa su tecnologie protettive che, immagino, siano spesso superate.
Ottimo lavoro! Ma anche il 2° grafico è un capolavoro...! 

Non ho modo di inserire le due barre, perche', dal testo di Alax, non si capisce, in totale, che percentuale di motociclisti usi le protezioni e che percentuale no.
Secondo me è il dato fondamentale per dare un senso allo studio. Comunque sul sito australiano segnalato da Alaxandair ci sono un bel po' di studi interessanti ai quali dedicarsi. Speriamo riportino dati un po' più comprensibili.
Ciau.
Si, e nello studio c'e' necessariamente, visto che e' necessario per calcolare le percentuali che poi hanno riportato male sul grafico.
Ragazzi, ho guardato i dati del grafico errato con un po' di calma: il dato mancante si puo' ricavare, se ben capisco cosa significano i dati dal testo esplicativo postato da Alax.
-- Abbiamo la percentuale dei >feriti< e la percentuale dei >feriti sprotetti< (le due curve nel grafico che ho postato)
-- sappiamo che la percentuale dei >feriti sprotetti< equivale alla percentuale (che abbiamo: barra 1) di >tutti gli sprotetti< (X) in circolazione, per cui dovremmo poter ricavare (X) con un semplice calcolo.
Ora ci provo e nel caso aggiorno il grafico.
Ecco il calcolo:
X = { 25.11- 0.16 * (y) } / 0.43
(secondo quello che avevi scritto prima)
Sono abituato a calcolare il rapporto decelerazione /coefficiente di attrito anche durante le frenate, questi calcoli ormai li faccio a mente.
MotoMatematica.com

P.s Taym ormai sta trasformando il sito in un sistema matematico. 

e voi ancora che gli andate appresso... 
Grafico aggiornato con barre
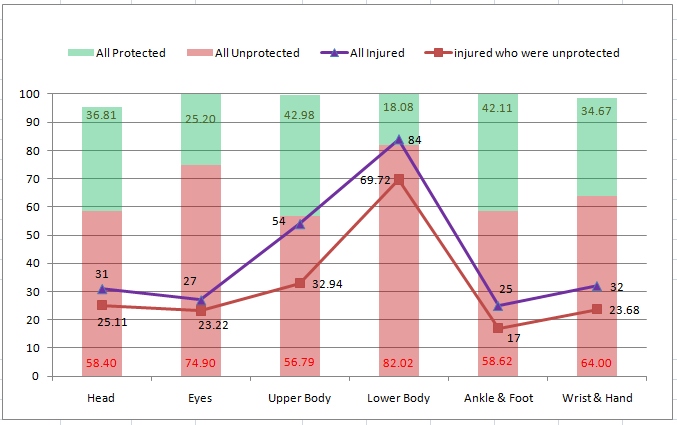
Notate che:
1.
Ho sovrapposto e non affiancato le barre in modo da chiarire meglio cosa significano. Esse, infatti, stando al testo riportato da Alax, rappresentano la percentuale di protetti e sprotetti sul TOTALE dei motociclisti in circolazione. Dunque come vedete la loro somma (verticalmente) finisce per coprire il 100% della popolazione dei motociclisti. Ora, come visibile in 3 casi, non si copre esattamente il 100%. Non posso sapere come mai, e possiamo supporre cio' dipenda da approssimazioni nel testo o piccoli errori.
Ora, cmq, mi sembra tutto piu' graficamente sensato.
Le barre rappresentano la popolazione nel suo complesso, suddivisa tra protetti e sprotetti.
Le curve (o linee spezzate) rappresentano i feriti; tutti (linea blue) e sprotetti (linea rossa). Notate che gli sprotetti, come dicevamo, costituiscono la maggioranza di tutti i feriti, che e' come dire che la linea rossa e' sempre piuttosto vicina alla blu. La distanza tra rossa e blue costituisce i feriti protetti che sono, appunto, pochi.
2.
Per Fra: la formula che ho usato e' piu' semplicemente, facendo riferimento al primo punto:
(X) = Totale Motociclisti Senza Casco = 25.11 / 43 * 100 = 58.40
che deriva dal fatto che sappiamo che il 43% del totale dei motociclisti senza casco equivale ai 23.11 % di motociclisti senza casco feritisi (sempre se leggiamo bene il testo).
A sostegno di questa interpretazione sta il fatto che calcolando
(Y) = Totale Motociclisti Con Casco = (31-25.11)/16*100 = 36.81 che, sommato a 58.40, si avvicina abbastanza al totale.
Facendo la stessa cosa con le altre parti del corpo andiamo anche piu' vicino al 100%, in alcuni casi raggiungendolo con esattezza.
Quindi accontentiamoci, considerando dal caos da cui siamo partiti 
3.
Qui trovate lo studio completo in download, per chi fosse interessato:
http://www.ilquen.it/download/miscellanea/MOTORCYCLE_ACCIDENT_CAUSE_FACT...
Sono oltre 400 pagine, per cui gli ho dato solo una scorsa molto molto rapida, e ne ho ricavato che
4.
Sebbene accurato e ben realizzato (e' un vero studio), e' estremamente vecchio.
Informazioni chiave per comprendere il senso di tale studio e quanto sia datato, sono:
- Il campione analizzato e' costituito da incidenti registrati dal LAPD, dipartimento di polizia di Los Angeles, ed un'istituzione statale altra di cui non ricordo il nome, della stessa area geografica, e si riferisce a Los Angeles e territorio circostante.
- Il campione e' stato raccolto negli anni 1978-1979 ! Certo, gran complimenti per l'approccio di assoluta avanguardia dei tempi...
- Il concetto di "indumenti protettivi" e' estremamente >>primitivo<< rispetto al nostro.
Ad esempio ho letto che gli indumenti del torso ed in generale della parte superiore del corpo erano considerati "protettivi" solo in virtu' della loro >>visibilita'<< . Dunque, i dati non tengono affatto conto, perche' molto probabilmente nel '78 non erano diffuse affatto, di protezioni all'impatto; men che mai di dati sull'abrasione.
I caschi, invece, ad esempio, sono stati ben analizzati, anche in laboratorio. Ma potete ben immaginare quanto un casco del '78 fosse meno protettivo, sia per materiali che per forma, rispetto ad uno attuale. Sono pressoche' certo che a Los Angeles nel '78 il 90% dei caschi fosse a scodella o aperto, da abbinarsi ad occhialoni - da cui il riferimento alla protezione degli occhi come parte del corpo separata.
Insomma, ragazzi, comprendiamo bene che se le cose stanno cosi', da un lato possiamo supporre che i feriti con indumenti protettivi, oggi, sarebbero molto meno percentualmente grazie alle migliori protezioni; per contro, Los angeles significa stradoni larghi e dritti, e velocita' inferiori, rispetto ad uno scenario europeo ed in particolare italiano attuale.
Direi che preso cosi' da solo ormai ha poca utilita', ma se ragionevolmente proiettato ai giorni nostri mi sembra sia invece ricco di informazioni utili per lo meno a confermare l'idea anche solo istintiva che abbiamo dell'utilita' delle protezioni. In tal senso cio' che colpisce sono le due linee.
Le barre hanno piu' che altro, ormai, un valore storico e ci dicono come si abbigliava la gente nel '78 per andare in moto (e che prezzo pagavano per essere poco protetti).
Ad ogni modo, spero la cosa vi sia utile. Se qualcuno poi avesse voglia di leggersi le 400 pagine... 
- Login per inviare commenti







